

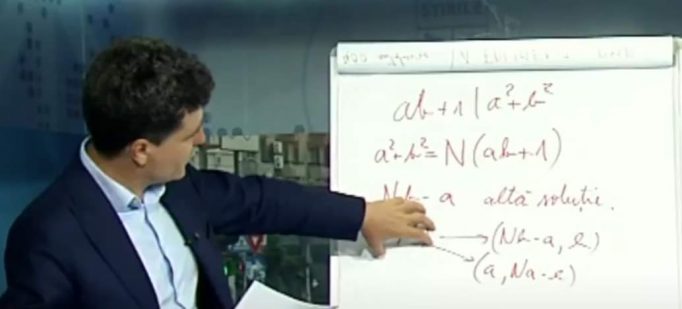
Nicușor Dan, candidat la Primăria Capitalei, a fost provocat să rezolve o problemă de matematică, într-o emisiune difuzată de postul de televiziune B1.
El și-a amintit de vremurile în care era olimpic internațional la matematică. Pe pagina sa de Facebook, Nicușor Dan a dat și soluția problemei respective.
Postarea integrală a lui Nicușor Dan:
Adrian Georgescu m-a provocat să rezolv o problemă pe care am rezolvat-o la Olimpiada Internațională de MatematicăMatematică din 1988. Răzvan Zamfir m-a invitat să o rezolv aseară la B1.
Rezolvând-o, mi-am amintit de emoțiile de atunci și de naivitatea cu care credeam, toți cei din lotul de matematică, că să câștigi Olimpiada este cel mai important lucru pe care poți să-l faci în viață.
Am făcut matematică, inițial dintr-o ambiție specifică adolescenței, apoi fascinat să cunosc descoperirile marilor înaintași.
Matematica este actul de cunoaștere care pune ordine, structură, în lumea reală. Matematica m-a format, m-a structurat. Cu formația de matematician, nu mi-e frică de nicio problemă complexă, iar administrarea Primăriei Capitalei este o problemă complexă.
Mulțumesc deci lui Adrian Georgescu și lui Răzvan Zamfir că m-au facut să mă întorc în timp, în lumea frumoasă și naivă de atunci.
Pentru pasionați, iată soluția:
Problemă: Demonstrați că dacă a, b sunt întregi pozitivi, iar ab+1 divide a^2+b^2, atunci raportul (a^2+b^2)/(ab+1) este pătrat perfect.
Soluția: Scriem a^2+b^2 = N(ab+1). Vom demonstra ca N este pătrat perfect.
Observăm [această observație este cea mai importantă în rezolvare] că relația de mai sus este o ecuație de gradul 2 în a, a^2 – Nba + b^2 – N = 0
Cealaltă soluție este Nb-a, conform formulei care dă suma celor două rădăcini ale ecuației de gradul 2 (Nb în cazul nostru).
Deci dacă (a, b) este o soluție, atunci (Nb-a, b) este o soluție.
Considerăm o soluție (a,b), și pentru că ecuația este simetrică în a și b, putem presupune că a este mai mare sau egal cu b.
Avem 3 cazuri:
i. Dacă b^2 – N = 0, problema este rezolvată, căci N = b^2 este pătrat perfect.
ii. Dacă b^2 – N > 0, folosim a doua relație între rădăcinile ecuației de gradul 2, a(Nb-a) = b^2 – N. Rezultă pe de o parte ca Nb-a este pozitiv. Pe de alta parte b^2 – N este mai mic decât b^2 și a este mai mare sau egal cu b, deci Nb-a este mai mic decât a. Rezultă că de la o soluție (a,b) am obținut o soluție (Nb-a, b) mai “mică”, adică (Nb-a) + b < a + b. [asta a fost a doua observație importantă pentru rezolvare]
iii. Dacă b^2 – N > 0, folosim a doua relație între rădăcinile ecuației de gradul 2, a(Nb-a) = b^2 – N. Rezultă că Nb-a este negativ, deci ca a > Nb. [aici intervine a treia observație/intuiție, cu cât raportul a/b este mai mare, cu atât numărul (a^2+b^2)/(ab+1) este mai mare, și pare că va fi prea mare]. În acest caz avem
(a^2+b^2)/(ab+1) = (a^2+b^2)/ab x ab/(ab+1) = (a/b + b/a) (1-1/ab)
Din ipoteza (a/b + b/a) este cel puțin (N+1/N) iar (1-1/ab) este cel puțin (1-1/N^3).
Cu un calcul scurt rezultă că (a^2+b^2)/(ab+1) este mai mare decât N, contrar ipotezei.
Cu asta, problema este rezolvată. Am văzut că dacă (a,b) este o soluție și N nu este pătrat perfect găsim o soluție mai mică. Considerăm soluția (a,b) cea mai mică. Întrucât nu există soluție mai mică, rezultă că N este pătrat perfect.